在物理学的广袤领域中,扭转运动是一种独特而重要的运动形式,它不仅在基础物理研究中占据着重要地位,更是在现代科技和日常生活中有着广泛而深刻的应用。
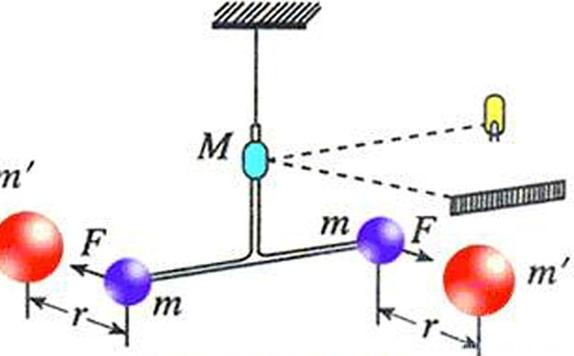
扭转运动的基本概念
扭转运动是指物体围绕某一固定轴线进行旋转的运动,这种运动可以由多种方式产生,例如施加一个扭矩,扭矩是使物体产生扭转的力,它的大小和方向决定了物体扭转的效果,当一个物体受到扭矩作用时,根据牛顿第二定律的角动量形式,物体将获得一个角加速度,从而开始或改变其扭转运动。
从力学角度来看,扭转运动涉及到许多基本的物理量,除了前面提到的扭矩和角加速度外,还有转动惯量,转动惯量是描述物体在扭转运动中惯性大小的物理量,它取决于物体的质量分布和转轴的位置,对于不同形状和质量分布的物体,其转动惯量的计算方法也有所不同,对于一个均匀细棒绕其中心轴的转动惯量和一个实心圆盘绕其中心轴的转动惯量就有明显的差异。
扭转运动的物理原理
扭转运动遵循一系列基本的物理定律,能量守恒定律在扭转运动中起着重要作用,当对一个物体施加扭矩使其扭转时,外力所做的功转化为物体的转动动能和弹性势能(如果物体具有弹性变形),在没有外界阻尼的情况下,物体的转动动能和弹性势能之间会相互转化,但总能量保持不变。
角动量守恒定律也是扭转运动中的一个重要原理,当一个系统不受外力矩或所受外力矩之和为零时,系统的总角动量保持不变,这个定律在许多物理现象和技术应用中都有体现,例如陀螺仪的工作原理就是基于角动量守恒。
扭转运动的实际应用
扭转运动在日常生活和现代科技中有着广泛的应用。
在交通工具领域,汽车的发动机通过燃烧燃料产生动力,经过一系列的传动装置将动力传递到车轮上,使车轮产生扭转运动,从而实现车辆的行驶,同样,飞机的螺旋桨也是通过发动机的驱动产生扭转运动,为飞机提供前进的动力。
在机械加工领域,各种机床上的刀具和工件之间的相对扭转运动是实现切削加工的关键,车床通过主轴带动工件旋转,同时刀具相对于工件进行切削运动,从而实现对工件的加工成型。
扭转运动还应用于许多其他领域,如发电机、电动机、钟表等,发电机通过机械装置驱动转子旋转,使磁极产生旋转磁场,从而在定子绕组中感应出电动势,实现电能的产生;电动机则是相反的过程,通过通电绕组产生磁场,与永磁体或电枢磁场相互作用,使转子产生扭转运动,从而实现机械能的输出。
扭转运动的研究意义
对扭转运动的研究不仅有助于我们深入理解物理世界的基本原理,还为推动科技进步和发展提供了重要的理论支持,随着科技的不断发展,对扭转运动的控制和应用也在不断创新和完善,在微机电系统(MEMS)领域,人们利用微小的扭转运动来实现各种传感器、执行器和微机械器件的功能,这些器件在生物医学、航空航天、通信等领域有着广泛的应用前景。
扭转运动作为物理世界中的一种基本运动形式,具有丰富而深刻的内涵和广泛的应用价值,通过对扭转运动的研究和探索,我们能够更好地认识和改造世界,为人类的发展和进步做出更大的贡献。
